作为精控强化的主要的方法，通过压缩空气推动丸料的喷丸得到了快速的发展。丸料通过喷嘴中的压缩空气进行加速。喷嘴中气流的速度可以达到声速，即在20℃的温度下达到340m/s。丸料可以通过以下三种中任意一种的方式和压缩空气汇合，即虹吸式、重力式或者直接供料式。喷出的丸料速度一般可以达到100m/s。
丸料的速度决定了丸料的能量（能量公式1/2mv2），即决定了喷丸强度。要达到喷丸的有效性和可控性的目的，和其它的参数相比，丸粒的速度是我们要控制的参数。能够影响丸粒速度的几个参数都需要进行控制。空气流和丸粒的速度可通过流体力学和弹道学进行研究。大学图书馆里的一排排教科书默默见证了这些学科的 复杂性。现在，我们对定量地分析丸粒加速的影响因素有着实际的需求。
喷丸的丸料加速过程可以分为以下三个阶段：
1-压缩空气流，
2-丸料混入压缩空气流，
3-丸料通过压缩空气流进行加速。
本文列出了一个一般方程可以用于预测丸料尺寸、形状和喷嘴中的压缩空气压力对于丸料速度的影响。
1 空气流
1.1压缩空气
如果让丸料加速，那么要有充足的压缩空气供应。对于不同直径的喷嘴所需要的气体供应量，喷嘴制造商有相关的手册进行介绍。同时手册也会介绍如果要使喷嘴中的空气压力稳定在一个范围，空气压缩的效率（压缩比）也应该有相应的要求。不幸的是，空气压缩的效率经常使用一个比较模糊的单位，比如“CFM”（立方英尺每分钟）。工业上比较清晰的单位是“SCFM”（标准立方英尺每分钟），该单位前面的“标准”加入了一些限定的条件，比如1.0 atm（1.0标准大气压，14.7 psi）、温度20℃以及36%的湿度。“ACFM”是实际立方英尺每分钟，表示每分钟通入管道的压缩空气的实际流量，该单位并不考虑压缩比。例如，如果一个压缩机在1个标准大气压下吸入的空气流量为100CFM，然后压缩成5个标准大气压的压缩空气，那么输入的流量为100SCFM，输出的流量为20ACFM。
压力表显示的数值与大气环境相关，而不仅仅是压力值。这意味着如果没有任何压力，那么压力表的读数为零。压缩比用CR表示，那么CR=（1+P），其中P表示的是在大气环境下的压力表的读数。
在大气环境下的空气的密度大约为1.2Kgm-3。如果我们对空气再额外地加压一个大气压（14.7psi），即P=1，那么CR=2，压缩空气的密度相应地增加了一倍。如果我们对空气加压到7个大气压的压力，那么压缩空气的密度需要乘以8。一般情况下，压缩空气的密度为CR乘以1.2Kgm-3。这就是喷丸设备中通入供气管道里的“沉重的空气”。图1说明了“沉重的空气”的制造过程。
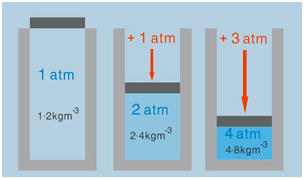图1. 外部的压力造成内部“沉重的空气”，atm=标准大气压
1.2管道中的空气流
从空气压缩机中出来的压缩空气进入到储气罐中并输送到空气输送管道中，应在输送之前经过空气干燥设备（例如冷干机）进行除水干燥。压缩空气会沿着管道流动，然后通到丸料供给系统和喷嘴系统中。压力罐可以使压缩机出来的波动的压缩空气变得平稳并能够对压缩空气进行储存。需要在空气供应系统中布置一个或多个压力控制阀（PCV）。压缩空气在管道的开始处的压力为P1，经过长为L的管道输送后，在末端的喷嘴处的压力为P2，如图2所示。
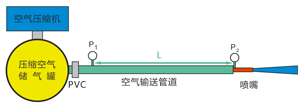图2. 压缩空气输送过程示意图（非真实比例图）
压力控制阀是空气压力的主要的控制机构。如果增加压力，我们期望软管中的空气流速也会增加。我们需要考虑的一个重要的因素就是空气压缩机的额定功率到底有多大。空气压缩机把空气充入储气罐的速度一定要高于实际使用掉的速度。我们可以拿汽车上的发电机和蓄电池系统进行类比。如果蓄电池的的输出量一直大于发电机的输入量，那么我们只能得到一个缺电的蓄电池。
我们可以把空气流速比作电流。要计算出电流，我们需要知道一个电线两端的势差。同样地，要计算出空气流速，我们需要知道空气输送管道两端的压力差。例如，（P1- P2）是空气输送管道两端的压力差，由该压力差引起的空气流速为Q。（P1- P2）是有用的工艺控制参数。（P1- P2）的变化可以是突发的，也可以是渐变的。如果（P1- P2）= P1，那么软管可能破裂了，如果（P1- P2）= 0，那么丸料可能在喷嘴处堵塞了。在实际使用中，（P1- P2）发生逐渐变化的原因是由于喷嘴逐渐磨损。如果喷嘴的直径增加，那么（P1- P2）会逐渐增加（假设P1一直维持在一个恒定的值，P1恒定在工业上是很容易实现的）。
值得注意的是，压降（P1- P2）意味着“能量损失”。在空气输送管道中以一个恒定的速度推动空气做的功为W，W=P.V，其中V表示空气的体积。“有用的能量”主要是在管道尾端的喷嘴处起作用，用P2.V表示。因此“能量损失”可以用（P1- P2）.V表示。
从上述可知，我们可以减少（P1- P2）来节能。首先与能量损失有关的参数是软管的长度L，能量损失与L成正比，因此应该避免使用过长的软管。另外一个与能量损失有关的重要参数是软管的内径D。对于给定的空气流速，压降和D4成反比（仅是一个大约的关系）。把软管的直径增加一倍，那么压降可以下降十六倍，然而如果把软管的长度缩短一倍，压降也只能将一倍。
1.3喷嘴中的空气流
我们第二个需求就是在喷嘴中对空气流进行加速。有一个流体加速的机理是大家比较熟悉的。如果在花园浇花，我们会发现软管中水流的速度比较慢。但是当水流到达喷嘴处时，如果喷嘴的横截面积是软管的1/4倍，那么水流的速度将在喷嘴处增加4倍。该原理同样适用气流加速，直至气流的速度达到临界值（声速）。图3解释了上述原理。
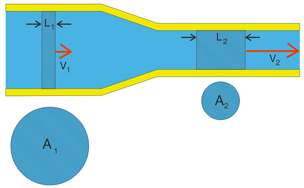图3. 压缩空气从管道到达喷嘴的过程中速度发生的变化
如图3所示，假设管道中有一个圆柱体的空气，体积为A1.L1，此时的速度为v1。当该圆柱体的空气到达喷嘴里面时，其体积没有发生变化（假设空气的密度没有发生变化），但是其尺寸发生了变化，截面积为A2、长度为L2以及速度为v2。既然A1.L1= A2.L2，那么v2= v1.A1/A2。如果v1.A1=Q，那么我们可以得到下式：v2=Q/A2 （1）
如果Q为10升/秒，喷嘴的横截面积为40mm2，那么由公式（1）可以得出v2为250m/s。该值为空气在喷嘴中的一个横截面的平均速度，实际上在该横截面的不同位置，空气的速度是不同的。
公式（1）仅在v2达到极限值之前适用，在实际过程中，喷嘴的空气压力通常非常高以至于会产生“阻塞流”。图4用了一个简单的图示说明了随着喷嘴中空气压力的增加空气速度发生的变化（假设喷嘴外部周围的大气压力为1atm）。和喷丸系统中其它区域不同，喷嘴中压力会产生一定的压力差，造成在喷嘴的狭窄位置产生“音障”的现象。当压力差达到1.9atm时，“音障”的现象就会出现。因为在所有的实际喷丸的过程中，喷嘴中的压力差都会超过2atm（29.4psi），无论喷嘴中空气压力和喷嘴直径有多大或多小，那么在喷嘴中的空气速度都将会达到一个固定的极限值。当然，前提是压缩空气的供应要充足。
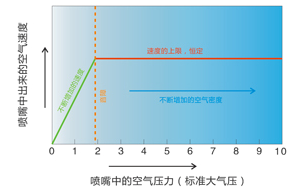图4. 压缩空气速度与压力的变化关系
如果喷嘴中的压缩空气达到了一个极限恒定值，我们就要问了，“如果空气压力的增加不影响空气的速度的话，那么会影响什么呢？”。答案是当压力进一步增加时，空气将进一步得到压缩，所以空气有着更高的密度，但速度还是一样的。喷嘴压力的增加只能使空气的“质量流量”增加。换句话说，“当喷嘴中空气压力增加时，喷出来的是更重的空气，但空气的速度是一样的”。
喷嘴中压缩空气的速度极限值取决于喷嘴的设计方式并可以从喷嘴制造商提供的“喷嘴性能表”中找到相关的数值。一般情况下，无论喷嘴中的压力和直径的大小，喷嘴中空气的速度为207±1m/s（678±2fps）。喷嘴中压缩空气的速度可以用气体流量除以压缩比得到ACFM，然后在除以喷嘴的横截面积。
表1显示了根据制造商的数据用Excel电子表格计算出的一些数据。电子表的列用A、B、C和D表示，9仅仅是表示了Excel中行的位置，便于计算出结果。
表1 从喷嘴中出来的压缩空气速度计算方法
喷嘴中的空气压力-atm（psi）压缩空气流量-升/秒(立方英尺/分钟)喷枪直径-毫米（英寸）平均空气速度-米/秒（英尺/秒）6.8 (100)204 (432.6)12.7 (0.5)206 (678)3.4 (50)115 (243.6)206 (676)6.8 (100)51 (108.2)6.35 (0.25)206 (680)3.4 (50)29 (61 .2)208 (680)ABCD
*-=(B9*1000/((A9+1)*(3.142*C9∧ 2/4)))
在喷嘴中横截面的不同位置速度变化很大，速度可达340m/s（音速），在喷嘴壁的位置的速度仅为0m/s。平均下来得到的速度为207m/s。
值得注意的是，在软管和喷嘴中经常会遇到“湍流”的现象（湍流的反义词为层流）。造成“湍流”的原因是雷诺数的值是非常大的。湍流的示意图如图5所示。空气在三维空间里顺着弯曲的路径流动，但总的趋势是往前方流动。
图5. 在管道或喷嘴中湍流状态下的压缩空气轨迹
2 丸料和压缩空气的混合过程
丸料和压缩空气的三种常见的混合系统是虹吸式系统、重力式系统和直接供料系统。
2.1虹吸式系统
该系统如图6所示。由于压缩空气的速度v2比丸料输送管道中的速度v1大的多，那么丸料输送管道中的空气会被吸入到压缩空气管道中，这就是“虹吸”这个词的来源。由于v1小于v2，那么丸料输送管道的空气压力要高于喷嘴中的压力。伯努利解释了这种现象，因此也称为伯努利定理。如果用p1表示丸料输送系统中的压力，用p2表示喷嘴中的压力，那么我们可以得到：(p1-p2)=1/2.ρA.(v22-v12) （2）其中ρA表示空气的密度。
（v22-v12）的值非常大，可以预测（p1- p2）的值也会非常大。
丸料输送管道中的速度v1足够把丸料“拖拽”到喷嘴中。同时压缩空气的紊流状态便于更好地把丸料和空气混合在一起。
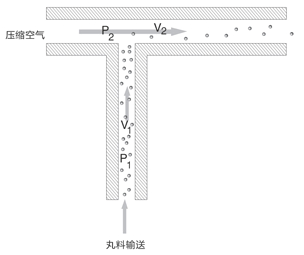图6. 虹吸式系统
2.2重力式系统
重力式系统和虹吸式系统相似的地方在于丸料是被输送到喷嘴中，不同的地方在于丸料输送管道的入口在喷嘴的上方，所以可以结合丸料本身重力的作用和虹吸的作用一起把丸料推送到喷嘴中。因此我们可以预测重力式系统与虹吸式系统相比，其丸料的给料速度更快。重力式系统如图7所示。丸料输送的角度为45°，该角度能够更好地使压缩空气和丸料混合。
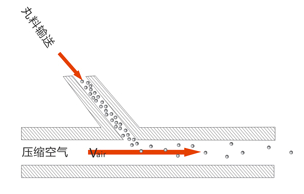图7. 重力给料喷嘴的示意图
2.2直接供料系统
在直接供料系统中，空气和丸料在进入喷丸软管之前就已经混合。在进入喷嘴之前，丸料和低速压缩空气的混合体一起向前推行。该系统如图8所示。贯穿该系统的紊流气流便于更好地把丸料和空气混合在一起。
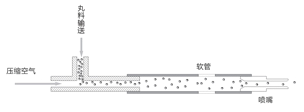图8. 直接供料系统（非真实比例图）
3 经过压缩空气加速后的丸料的速度
3.1加速
快速流动的压缩空气为每一个丸粒提供了一个加速的力量。当有不平衡的力存在时，加速作用就会发生。牛顿第二定律就是力等于质量乘以加速度，用下式表示为：F=m.a （3）
其中F是不平衡的力，m是质量，a是力F方向上的加速度。
图9表示了直通式喷嘴中空气和丸料状态模型。在喷嘴的中心部位压缩空气的速度高，当靠近喷嘴内壁时，压缩空气的速度会降低。我们在1.1章节中已经介绍到，对于直通式喷嘴，压缩空气的速度可以达到大约200m/s（656英尺/秒）。由于空气流的“紊流”作用，丸料将会在喷嘴中到处移动。因此我们可以假设每个丸粒上的轴向的平均的力F都是相同的。
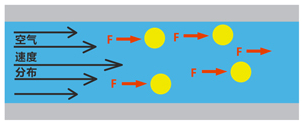图9. 直通式喷嘴中的空气和丸料的状态示意图
在虹吸式和重力式系统中，设定丸料加速的距离为s。直接供料系统中丸料加速的距离可以更长，丸料加速后的速度为vs。因为喷嘴中压缩空气的速度达到限值，所以丸料的加速作用主要发生在喷嘴里面。
如果我们假定丸料的加速作用是恒定的，那么我们可以得到下面的简单关系式：Vs2=2.a.s （4）
为了提高丸料的速度，我们可以增加丸料的加速作用或者增加加速距离或者同时增加上述两个参数。由于喷嘴的长度是有限的（一般长度为100mm），因此如果要使丸料的速度达到50m/s，那么对丸料的加速作用的要求非常高。如果把0.100m和50m/s代入到式（4）中，那么丸料的加速度a将会达到12500m.s-2，也就是自由加速度的1250倍。
我们可以把公式（3）变成a=F/m，然后代入公式（4），可得：Vs2=2.F.s/m （5）
那么在快速流动的流体中，作用在一个丸粒上的力F为：F=1/2.CD.A.ρA.(va-vs)2 （6）
其中CD是指“阻力系数”（该值是无量纲数，取决于物体的形状，对于一个光滑的球体CD≈0.5），A是指物体的横截面积，ρA是压缩空气的密度（压缩比乘以1.2Kgm-3），va是空气流的速度，vs是丸粒的速度。(va-vs)定义为丸粒相对于空气流的“相对速度”。
3.2丸料速度的发展过程
合并公式（5）和公式（6），可得：vs= (CD.A.ρA.s/m)0.5(va-vs) （7）
公式（7）可以用我们更加熟悉的形式进行表达，对于圆形的丸料，把A=π.d2/4和m=ρS.π.d3/6代入式（7）中，其中d是丸粒的直径，ρS是丸粒的密度，可得：vs=（1.5.CD. ρA.s/π.d. ρS）0.5(va-vs) （8）
利用已知的喷丸参数采用公式（8）可以计算出vs。简单的方法就是使用Excel电子表，把公式（8）重新整理一下。表2显示了如何用下面的公式计算出丸粒的速度：C11=C9*((1.5*C3*C5*C4*C8)/(C6*C7))^0.5/(1+((1.5*C3*C5*C4*C8)/(C6*C7))^0.5)
电子表可以简单方便地得出特定参数随变量的变化而变化的曲线。因此可以使用电子表得出丸粒的速度随其它参数变化的曲线。图10为根据公式（8）得出的丸粒速度随空气压力的变化曲线。
表2 使用Excel计算的从喷嘴中出来的丸料的速度
1BCD2参数数值单位3Cd0.5
4空气密度1.2kgm-35空气压力9atm6丸料密度7860kgm-37丸料直径0.25mm8长度50mm9空气速度200m.s-110
11丸料速度48.6m.s-1
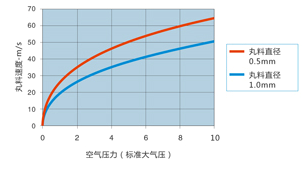图10. 丸料速度和空气压力的关系曲线
丸料加速过程一共有三个阶段，分别发生在以下三个部位：
（Ⅰ）丸料输送管道；
（Ⅱ）喷嘴；
（Ⅲ）离开喷嘴后的空气和丸料锥形区域。
（Ⅰ）丸料输送管道
直接送料式的软管长度与喷嘴的长度比起来要长得多，但是空气在软管中的速度与在喷嘴中比起来要慢得多。空气的速度可以用压缩空气进气量除以压缩比在除以软管的横截面积。例如，使用表1的电子表并把6.8atm（100psi）、204升/秒（432.6标准立方英尺/分钟）并把软管内径为25.4mm（1英寸）代入其中的公式可以得到软管中的空气速度为51.5m/s（170英尺/秒）。把软管的长度4000mm、空气压力6.8atm（100psi）以及空气速度51.5m/s代入表2的公式中可以得到丸粒的速度为11.2m/s。与后续的喷嘴中加速的过程相比，这个过程可以看作是在喷嘴前的预加速。如果我们使用是比较大的丸料和/或者需要把丸料速度提高到较快的话，预加速的作用是很重要的。
（Ⅱ）喷嘴
公式（8）可以用于预测两种不同尺寸弹丸的空气压力和出喷嘴后的速度的变化关系，如图10所示。对于大尺寸的丸料，喷嘴前的预加速的优势就显现出来了。该等式同样可以预测喷嘴长度和丸料材料（通过改变丸料密度）对丸料速度的影响。
（Ⅲ）离开喷嘴后的空气和丸料锥形区域。
一旦丸料从喷嘴中喷射出来之后，丸料的速度与气流的速度相比会慢很多。图11说明了丸料加速的区域为喷嘴内的A点到B点，压缩空气的速度是恒定的。在B点时，压缩空气的压力会出现一个快速的降低。从B点到C点，压缩空气的速度会降低，当到达C点时，压缩空气和丸料的速度将达到一致。过程再往后进行，丸料的飞行速度要比气流快，所以丸料的速度开始降低了。
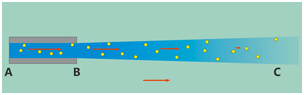图11丸料在喷嘴中的加速段A-B以及离开喷嘴后的B-C段的速度变化
在锥形区域BC段的丸料速度变化的理论分析是非常非常复杂的。有相关的试验数据显示在距离喷嘴200mm处丸料的速度将达到限值。举一个宽泛的例子，代入长度200mm、空气速度100m/s（平均值）以及空气压力1个大气压，可以得到丸料离开喷嘴后的速度为17.6m/s。喷枪的类型也是影响丸料速度的一个重要因素，拉伐尔喷嘴（收敛扩散形喷嘴）比直喷嘴对丸料的加速作用要大。
3.3丸料的速度
对于直接送料式系统，丸料在喷嘴出口处的速度是由（Ⅰ）和（Ⅱ）共同作用的结果。对于虹吸式和重力式系统，料在喷嘴出口处的速度仅是（Ⅱ）作用的结果。丸料离开喷嘴后速度的大小取决于离开喷嘴的距离，一般情况下会在距离喷嘴的某个位置达到速度限值（一般是距离200mm速度达到速度限值）。
讨论和结论
本篇文章是基于空气流和丸料加速过程的一个简单模型进行了讨论。由于忽略了温度和湿度的轻微影响，因此对于丸粒速度的准确预测是不可能完成的。另一方面本文中的公式可以用来解释试验得出的一些结果。
从本文中可以得到以下几个重要的结论：
•如果压缩空气的供应充足的话，那么喷嘴中的空气速度是几乎不变的。该速度几乎与音速相同且和喷嘴中的压力和直径没有关系。
•增加喷嘴中的空气压力会增加丸料的速度，这是因为空气的密度升高了。
•得到了一个一般公式（公式（8）），该公式可以预测丸料的速度和丸料尺寸、丸料密度、喷嘴长度以及喷嘴压力之间的变化关系。
